L'algorithme du lancer de rayons

La synthèse d'images est une transformation permettant de passer d'un espace objet, représentant la scène 2D ou 3D à visualiser, à un espace image 2D visualisant le contenu de la scène généralement sur un écran graphique. Les constituants de la scène sont des objets, résultant ou non de composition (intersection, union, ...) d'objets primitifs (sphères, cônes, cubes, ...). A ces objets sont associés des propriétés géométriques (emplacement dans la scène), ainsi que des propriétés photo-métriques (couleur, texture, ...). Les éléments de l'espace image sont quant à eux les pixels composants l'écran. L'algorithme revient alors, pour chacun des pixels, de calculer l'équation d'un rayon primaire, partant du point d'observation, et passant par le pixel dont on désire calculer l'illumination. Ce rayon sera ensuite projeté dans l'espace objet, et on testera l'intersection de l'équation de la droite ainsi obtenue avec l'ensemble des objets composants la scène. Lors de l'intersection de la droite avec un objet on aura à appliquer un modèle d'illumination tenant compte des différentes sources de lumière, ainsi que de rayons secondaires, provenant de la réflexion et de la réfraction du rayon sur l'objet. Ces rayons secondaires seront considérés comme des rayons, et on aura donc à tester leurs intersections avec les objets de la scène.

  
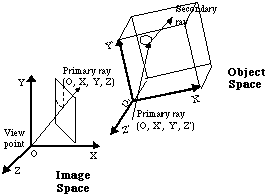
Figure 1: Le processus de synthèse d'images : passage d'un espace objet à un espace image

Cette procédure récursive conduit donc à la constitution d'un arbre des rayons à partir duquel on pourra calculer l'illumination du pixel origine. Dans le cadre de cet enseignement nous considérerons une version simplifiée de l'algorithme, par exemple en ne tenant compte que d'objets sphériques, sans composition entre objets, avec également un modèle d'illumination simplifié.

L'algorithme du lancer de rayons (voir Algorithme 2) est un algorithme permettant de synthétiser des images présentant un rendu réaliste. Toutefois il présente l'inconvénient de demander une puissance de calcul conséquente. Afin de réduire ce temps différentes solutions sont envisageables, dont l'utilisation du parallélisme ainsi que celle de processeurs spécialisés. Dans le cadre de ce module d'enseignement, un parallélisme sur les données sera mis en oeuvre, et parmi les deux solutions envisageables, partitionnement de image ou partitionnement de l'espace objet, nous avons retenu la première solution.

Outre ce parallélisme, le projet met en avant l'apport des solutions matérielles permettant, à coût identique, d'atteindre des accélérations supérieures. Une étude fait ressortir la nature extrêmement répétitive du calcul d'intersection. Il s'agit alors de faire effectuer par un ASIC conçu à cet effet, la primitive calcul d'intersection d'une droite avec une sphère (voir Algorithme 3). Le processeur programmable ayant alors pour rôle, outre le support de la ferme de processus, l'alimentation de l'ASIC en données.

Cet algorithme présente donc toutes les qualités pour le projet d'enseignement que nous avions. Il est pédagogiquement adapté au profil d'étudiants que nous avons, correspond à une application extraite du monde réel et permet donc d'intéresser ces étudiants au développement de systèmes électroniques. L'algorithme lui-même peut être simplifié, puis étendu depuis cette version initiale, ce qui permet une grande souplesse vis à vis du rythme des étudiants. Enfin les contraintes temps réel sont telles, qu'elles justifient une approche méthodologique utilisant différentes formes de parallélisme, et abordant des problèmes très contraignant comme la maîtrise de la charge de calcul effectuée sur les différents processeurs.

  
Figure 2: Algorithme de lancer de rayons

  
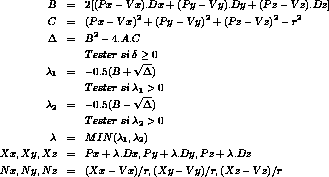
Figure 3: Coeur de l'algorithme de lancer de rayons : intersection d'un rayon avec une sphère